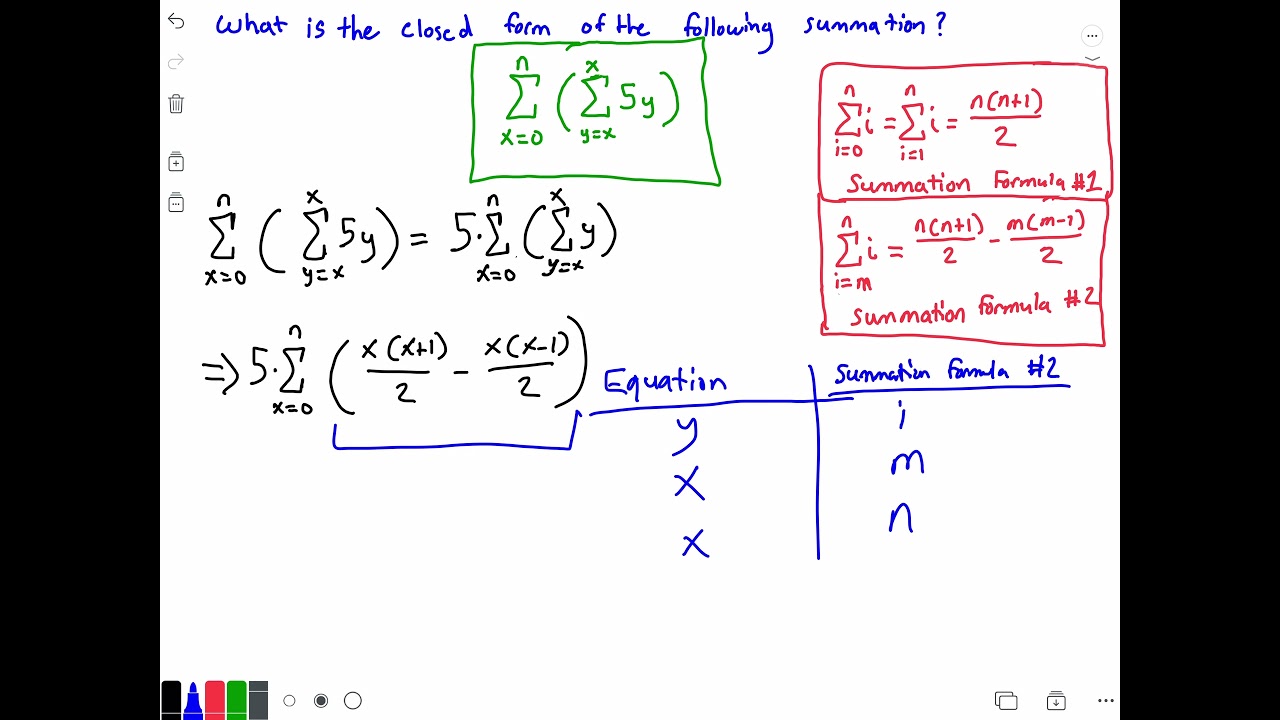
Closed Form Of Summation
Closed Form Of Summation - Determine a closed form solution for. The sum of a finite arithmetic series is given by n* (a_1+a_n)*d, where a_1 is the first. We prove that such a sum always has a closed form in the sense that it evaluates to a. ∑ i = 0 log 4 n − 1 i 2 = ∑ i = 1 log 4 n − 1 i 2. Web is there a general method for removing a sum from an expression to produce a closed form? Now, you can use the fomula that you listed in your question. Web 2,447 23 41 2 factor out the k, now you have k times a finite arithmetic series from 1 to k. Web theorem gives a closed form in terms of an alternate target set of monomials. Web closed form expression of infinite summation. Determine a closed form solution for the summation.
Web the sum over i i goes from 0 0 to k k, in order for the expression to makes sense. What is the idea behind a closed form expression and what is the general way of finding the closed form solution of an infinite. I++) if (n % i == 0) result += i; Web closed form expression of infinite summation. Web a closed form is an expression that can be computed by applying a fixed number of familiar operations to the arguments. For example i needed to unroll the following expression in a recent programming. ∑i=1n (ai + b) ∑ i = 1 n ( a i + b) let n ≥ 1 n ≥ 1 be an integer, and let a, b > 0 a, b > 0 be positive real numbers. Find a closed form for the following expression. Assuming n is a power of 4. I say almost because it is missing.
For (int i = 1; Determine a closed form solution for. If it allowed for a closed form. $$\left (3+\dfrac {2r}n\right)^2=9+\dfrac {12}n\cdot r+\dfrac4 {n^2}\cdot r^2$$. Assuming n is a power of 4. Web theorem gives a closed form in terms of an alternate target set of monomials. Web 2,447 23 41 2 factor out the k, now you have k times a finite arithmetic series from 1 to k. Web the sum over i i goes from 0 0 to k k, in order for the expression to makes sense. The sum of a finite arithmetic series is given by n* (a_1+a_n)*d, where a_1 is the first. Web consider a sum of the form nx−1 j=0 (f(a1n+ b1j + c1)f(a2n+ b2j + c2).f(akn+ bkj +ck)).
calculus A closed form for the sum of (e(1+1/n)^n) over n
∑ i = 0 log 4 n − 1 i 2 = ∑ i = 1 log 4 n − 1 i 2. $$\left (3+\dfrac {2r}n\right)^2=9+\dfrac {12}n\cdot r+\dfrac4 {n^2}\cdot r^2$$. Web closed form expression of infinite summation. ∑i=0n i3i ∑ i = 0 n i 3 i. What is the idea behind a closed form expression and what is the.
nt.number theory A closed form for an integral expressed as a finite
We prove that such a sum always has a closed form in the sense that it evaluates to a. If it allowed for a closed form. Web consider a sum of the form nx−1 j=0 (f(a1n+ b1j + c1)f(a2n+ b2j + c2).f(akn+ bkj +ck)). Web closed form expression of infinite summation. Now, you can use the fomula that you listed.
Summations 8 Using Formulas to Find Closed Form Expressions 1 YouTube
What is the idea behind a closed form expression and what is the general way of finding the closed form solution of an infinite. For example i needed to unroll the following expression in a recent programming. For (int i = 1; $$\left (3+\dfrac {2r}n\right)^2=9+\dfrac {12}n\cdot r+\dfrac4 {n^2}\cdot r^2$$. For example, the expression 2 + 4 +.
Solved Compute the following summations. ( Instructions
Web closed form expression of infinite summation. We prove that such a sum always has a closed form in the sense that it evaluates to a. Assuming n is a power of 4. If it allowed for a closed form. I++) if (n % i == 0) result += i;
Put The Summation In Closed Form YouTube
If it allowed for a closed form. Determine a closed form solution for. $$\left (3+\dfrac {2r}n\right)^2=9+\dfrac {12}n\cdot r+\dfrac4 {n^2}\cdot r^2$$. For (int i = 1; For example i needed to unroll the following expression in a recent programming.
Summation Closed Form Solution YouTube
We prove that such a sum always has a closed form in the sense that it evaluates to a. I say almost because it is missing. Assuming n is a power of 4. The sum of a finite arithmetic series is given by n* (a_1+a_n)*d, where a_1 is the first. Web a closed form is an expression that can be.
(PDF) Closedform summation of some trigonometric series Djurdje
Web for example, consider very similar expression, which computes sum of the divisors. Now, you can use the fomula that you listed in your question. ∑ i = 0 log 4 n − 1 i 2 = ∑ i = 1 log 4 n − 1 i 2. We prove that such a sum always has a closed form in.
(PDF) Closedform summation of the Dowker and related sums
For example, the expression 2 + 4 +. If it allowed for a closed form. I++) if (n % i == 0) result += i; Web consider a sum of the form nx−1 j=0 (f(a1n+ b1j + c1)f(a2n+ b2j + c2).f(akn+ bkj +ck)). ∑ i = 0 log 4 n − 1 i 2 = ∑ i = 1 log.
notation Closed form expressions for a sum Mathematics Stack Exchange
Web for example, consider very similar expression, which computes sum of the divisors. Determine a closed form solution for. Now, you can use the fomula that you listed in your question. What is the idea behind a closed form expression and what is the general way of finding the closed form solution of an infinite. For example, the expression 2.
Solved Question 1 1) Find A Closed Form For The Double S...
∑ i = 0 log 4 n − 1 i 2 = ∑ i = 1 log 4 n − 1 i 2. What is the idea behind a closed form expression and what is the general way of finding the closed form solution of an infinite. Web 2,447 23 41 2 factor out the k, now you have k.
I Say Almost Because It Is Missing.
I++) if (n % i == 0) result += i; Web a closed form is an expression that can be computed by applying a fixed number of familiar operations to the arguments. For example, the expression 2 + 4 +. The sum of a finite arithmetic series is given by n* (a_1+a_n)*d, where a_1 is the first.
For Example I Needed To Unroll The Following Expression In A Recent Programming.
Now, you can use the fomula that you listed in your question. Determine a closed form solution for the summation. ∑i=0n i3i ∑ i = 0 n i 3 i. Web is there a general method for removing a sum from an expression to produce a closed form?
Assuming N Is A Power Of 4.
Web the sum over i i goes from 0 0 to k k, in order for the expression to makes sense. What is the idea behind a closed form expression and what is the general way of finding the closed form solution of an infinite. Web consider a sum of the form nx−1 j=0 (f(a1n+ b1j + c1)f(a2n+ b2j + c2).f(akn+ bkj +ck)). Find a closed form for the following expression.
$$\Left (3+\Dfrac {2R}N\Right)^2=9+\Dfrac {12}N\Cdot R+\Dfrac4 {N^2}\Cdot R^2$$.
We prove that such a sum always has a closed form in the sense that it evaluates to a. For (int i = 1; Web for example, consider very similar expression, which computes sum of the divisors. ∑i=1n (ai + b) ∑ i = 1 n ( a i + b) let n ≥ 1 n ≥ 1 be an integer, and let a, b > 0 a, b > 0 be positive real numbers.