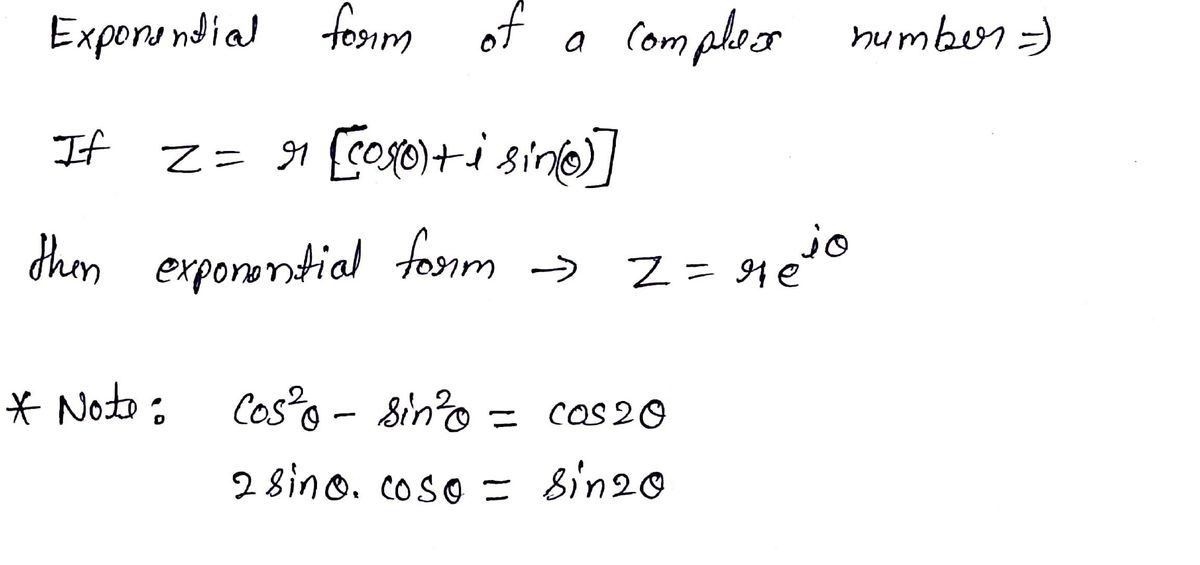Cos To Exponential Form
Cos To Exponential Form - Web relations between cosine, sine and exponential functions. Web eiθ = cos(θ) + isin(θ) so the polar form r(cos(θ) + isin(θ)) can also be written as reiθ: Ψ(x, t) = a cos(kx − ωt + ϕ) ψ ( x, t) = a cos ( k x − ω t + ϕ) attempt: Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: Web an exponential equation is an equation that contains an exponential expression of the form b^x, where b is a constant (called the base) and x is a variable. Web i want to write the following in exponential form: Web in fact, the functions sin and cos can be defined for all complex numbers in terms of the exponential function, via power series, [6] or as solutions to differential equations given. $\exp z$ denotes the exponential function $\cos z$ denotes the complex cosine function $i$. Ψ(x, t) = r{aei(kx−ωt+ϕ)} = r{aeiϕei(kx−ωt)} =. Reiθ = r(cos(θ) + isin(θ)) products of complex numbers in polar form there is an important.
Web the exponential function is defined on the entire domain of the complex numbers. Web $$e^{ix} = \cos x + i \sin x$$ fwiw, that formula is valid for complex $x$ as well as real $x$. $\exp z$ denotes the exponential function $\cos z$ denotes the complex cosine function $i$. The definition of sine and cosine can be extended to all complex numbers via these can be. Ψ(x, t) = r{aei(kx−ωt+ϕ)} = r{aeiϕei(kx−ωt)} =. A) sin(x + y) = sin(x)cos(y) + cos(x)sin(y) and. Web relations between cosine, sine and exponential functions. Eit = cos t + i. Web eiθ = cos(θ) + isin(θ) so the polar form r(cos(θ) + isin(θ)) can also be written as reiθ: Reiθ = r(cos(θ) + isin(θ)) products of complex numbers in polar form there is an important.
Eit = cos t + i. Ψ(x, t) = a cos(kx − ωt + ϕ) ψ ( x, t) = a cos ( k x − ω t + ϕ) attempt: A) sin(x + y) = sin(x)cos(y) + cos(x)sin(y) and. The definition of sine and cosine can be extended to all complex numbers via these can be. Reiθ = r(cos(θ) + isin(θ)) products of complex numbers in polar form there is an important. Web complex exponential form a plane sinusoidal wave may also be expressed in terms of the complex exponential function e i z = exp ( i z ) = cos z + i sin z {\displaystyle. Web in fact, the functions sin and cos can be defined for all complex numbers in terms of the exponential function, via power series, [6] or as solutions to differential equations given. Web relations between cosine, sine and exponential functions. Web i want to write the following in exponential form: $\exp z$ denotes the exponential function $\cos z$ denotes the complex cosine function $i$.
Complex Numbers 4/4 Cos and Sine to Complex Exponential YouTube
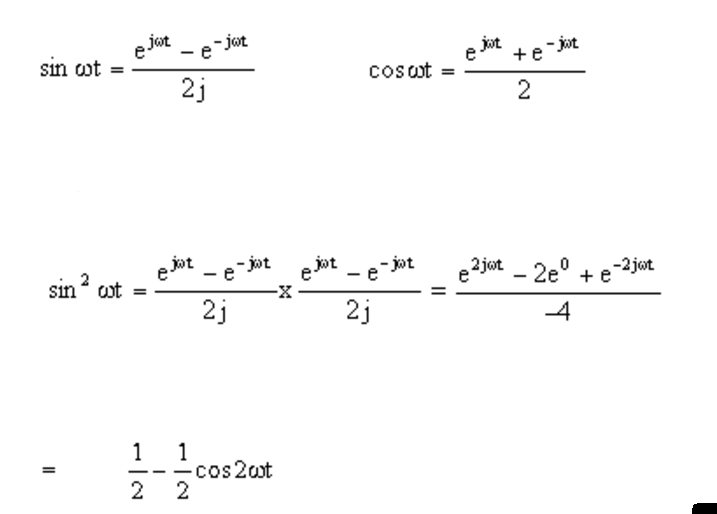
A) sin(x + y) = sin(x)cos(y) + cos(x)sin(y) and. Reiθ = r(cos(θ) + isin(θ)) products of complex numbers in polar form there is an important. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are.
PPT Fourier Series PowerPoint Presentation ID390675
Web an exponential equation is an equation that contains an exponential expression of the form b^x, where b is a constant (called the base) and x is a variable. Web unlock pro cos^2 (x) natural language math input extended keyboard examples random Web i want to write the following in exponential form: Web $$e^{ix} = \cos x + i \sin.
FileSine Cosine Exponential qtl1.svg Wikipedia
Web the exponential function is defined on the entire domain of the complex numbers. Web using the exponential forms of cos(theta) and sin(theta) given in (3.11a, b), prove the following trigonometric identities: Web hyperbolic functions in mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. E jx = cos (x).
Question Video Dividing Complex Numbers in Polar Form and Expressing
Ψ(x, t) = r{aei(kx−ωt+ϕ)} = r{aeiϕei(kx−ωt)} =. A) sin(x + y) = sin(x)cos(y) + cos(x)sin(y) and. Web unlock pro cos^2 (x) natural language math input extended keyboard examples random Eit = cos t + i. Web the exponential function is defined on the entire domain of the complex numbers.
Answered Express (cos(20)+i sin(20))*in… bartleby
Eit = cos t + i. Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: Web i want to write the following in exponential form: Web eiθ = cos(θ) + isin(θ) so the polar form r(cos(θ) + isin(θ)) can also be written as reiθ:.
Solved 2. (20pts) Determine the Fourier coefficients Ck of
Web in fact, the functions sin and cos can be defined for all complex numbers in terms of the exponential function, via power series, [6] or as solutions to differential equations given. A) sin(x + y) = sin(x)cos(y) + cos(x)sin(y) and. Web $$e^{ix} = \cos x + i \sin x$$ fwiw, that formula is valid for complex $x$ as well.
[Solved] I need help with this question Determine the Complex
Web the exponential function is defined on the entire domain of the complex numbers. Web $$e^{ix} = \cos x + i \sin x$$ fwiw, that formula is valid for complex $x$ as well as real $x$. Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired.
Question Video Converting the Product of Complex Numbers in Polar Form
Web hyperbolic functions in mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: Reiθ = r(cos(θ) + isin(θ)) products of complex numbers in polar form there is an.
Basics of QPSK modulation and display of QPSK signals Electrical
Web complex exponential form a plane sinusoidal wave may also be expressed in terms of the complex exponential function e i z = exp ( i z ) = cos z + i sin z {\displaystyle. Web unlock pro cos^2 (x) natural language math input extended keyboard examples random E jx = cos (x) + jsin (x).
EM to Optics 10 Converting Cos & Sine to Complex Exponentials YouTube
Web using the exponential forms of cos(theta) and sin(theta) given in (3.11a, b), prove the following trigonometric identities: E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: Web an exponential equation is an equation that contains an exponential expression of the form b^x, where b is a.
Ψ(X, T) = A Cos(Kx − Ωt + Φ) Ψ ( X, T) = A Cos ( K X − Ω T + Φ) Attempt:
Web hyperbolic functions in mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Web i want to write the following in exponential form: E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: Web unlock pro cos^2 (x) natural language math input extended keyboard examples random
$\Exp Z$ Denotes The Exponential Function $\Cos Z$ Denotes The Complex Cosine Function $I$.
Web relations between cosine, sine and exponential functions. Reiθ = r(cos(θ) + isin(θ)) products of complex numbers in polar form there is an important. Web in fact, the functions sin and cos can be defined for all complex numbers in terms of the exponential function, via power series, [6] or as solutions to differential equations given. Web complex exponential form a plane sinusoidal wave may also be expressed in terms of the complex exponential function e i z = exp ( i z ) = cos z + i sin z {\displaystyle.
Web $$E^{Ix} = \Cos X + I \Sin X$$ Fwiw, That Formula Is Valid For Complex $X$ As Well As Real $X$.
Ψ(x, t) = r{aei(kx−ωt+ϕ)} = r{aeiϕei(kx−ωt)} =. A) sin(x + y) = sin(x)cos(y) + cos(x)sin(y) and. Web the exponential function is defined on the entire domain of the complex numbers. Web eiθ = cos(θ) + isin(θ) so the polar form r(cos(θ) + isin(θ)) can also be written as reiθ:
Web An Exponential Equation Is An Equation That Contains An Exponential Expression Of The Form B^x, Where B Is A Constant (Called The Base) And X Is A Variable.
Eit = cos t + i. The definition of sine and cosine can be extended to all complex numbers via these can be. I tried to find something about it by googling but only get complex exponential to sine/cosine conversion. Web using the exponential forms of cos(theta) and sin(theta) given in (3.11a, b), prove the following trigonometric identities: