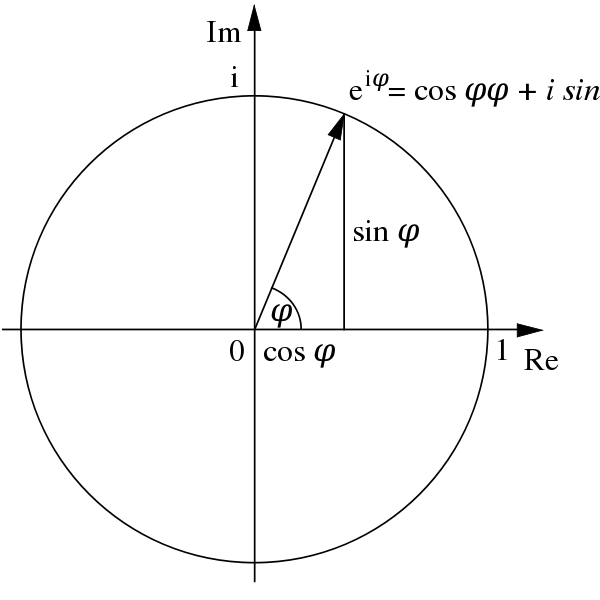
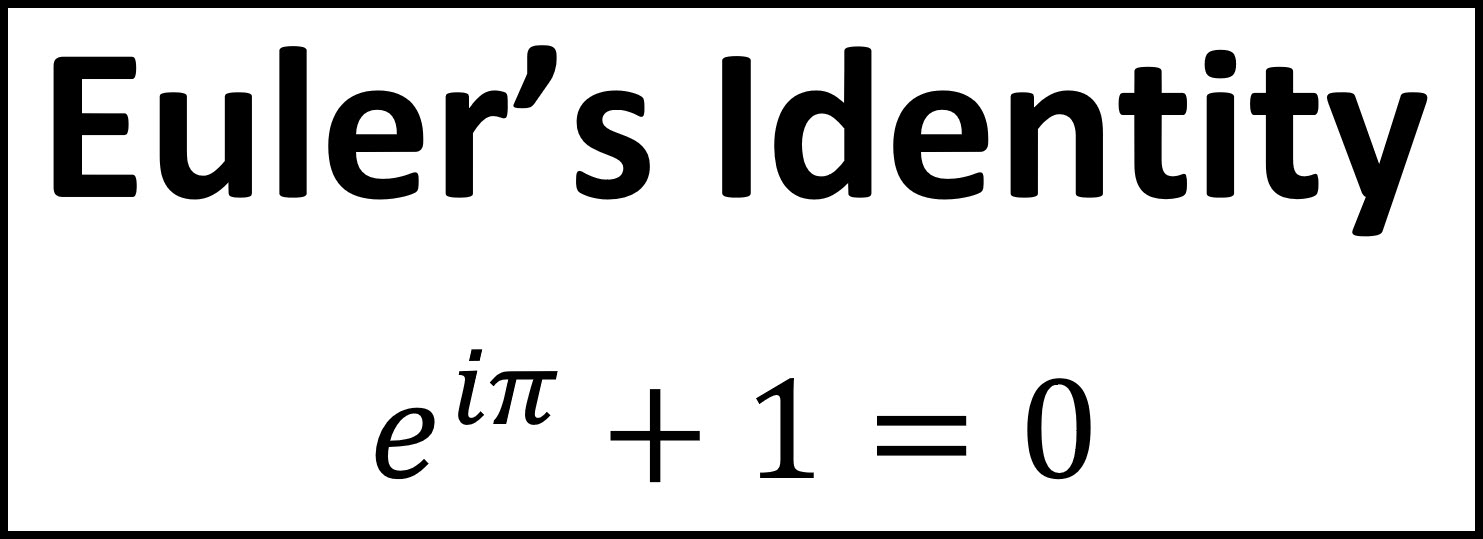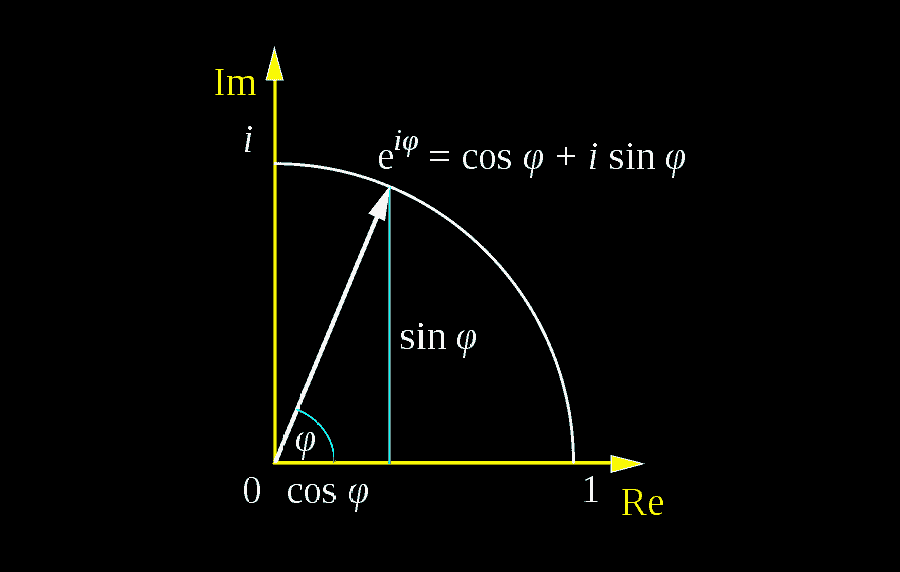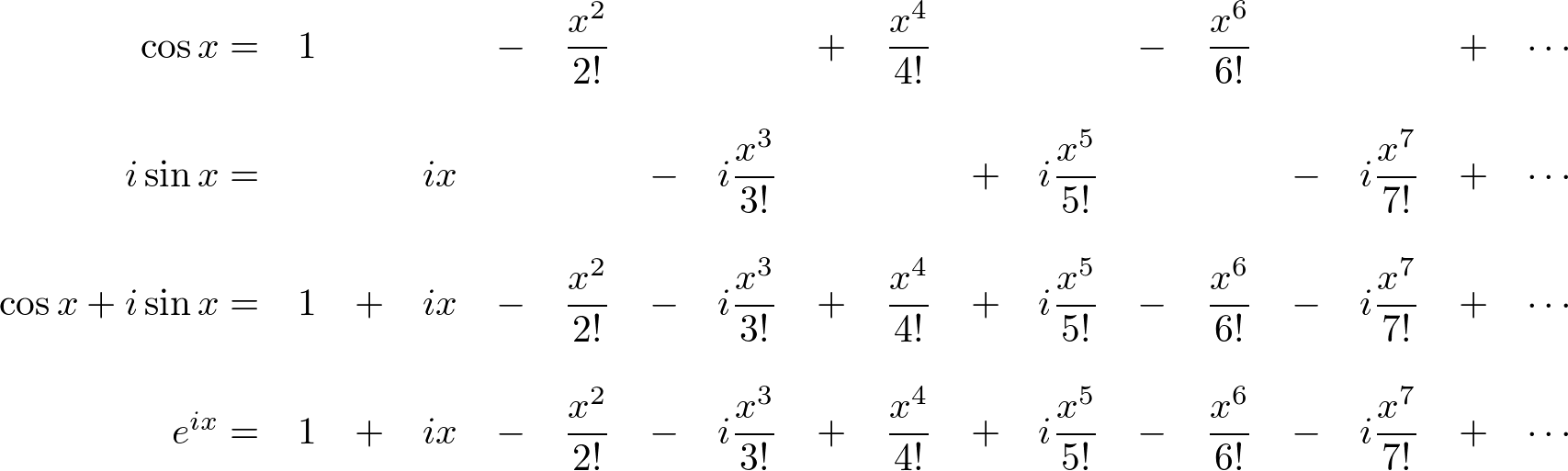Cosine In Euler Form
Cosine In Euler Form - Let me try this from a different angle: Web in complex analysis, the hyperbolic functions arise when applying the ordinary sine and cosine functions to an imaginary angle. Web euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. This formula is the most important tool in ac analysis. Web finally, there is a nice formula discovered by leonhard euler in the 1700s that allows us to relate complex numbers, trigonometric functions and exponents into one single formula:. It is why electrical engineers need to. Web euler's formula can be used to prove the addition formula for both sines and cosines as well as the double angle formula (for the addition formula, consider $\mathrm{e^{ix}}$. Web euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: E i x = cos x + i sin x. Using these formulas, we can.
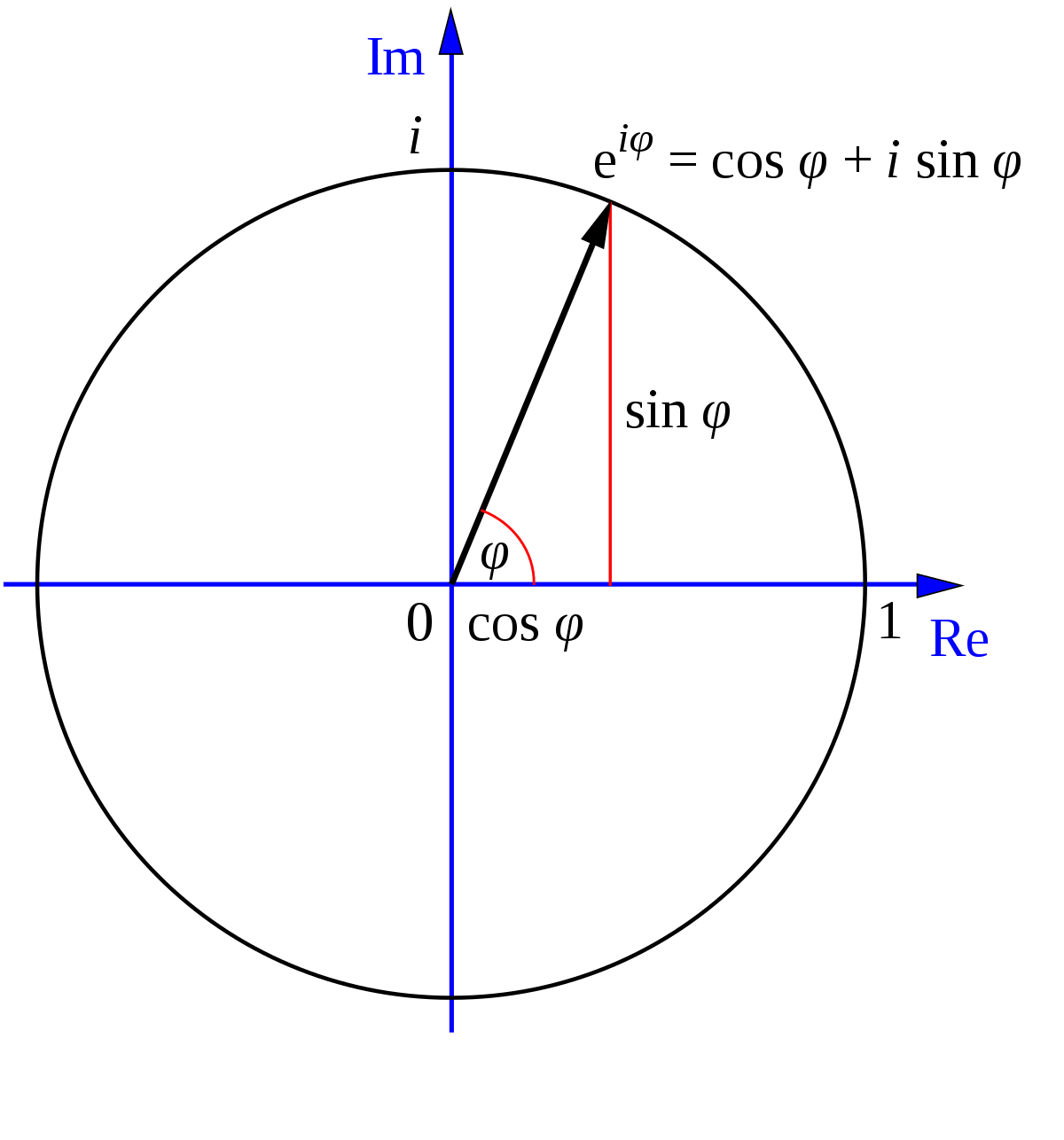
Suppose we have a function ∠\theta=\cos\theta+i\sin\theta; The simple derivation uses euler's formula. That is, it defines a complex number that is one unit away. Web euler's formula relates sine and cosine to the exponential function: Web answer (1 of 9): Web sine and cosine emerge from vector sum of three spinning numbers in euler’s formula, the green spinning number is. Web finally, there is a nice formula discovered by leonhard euler in the 1700s that allows us to relate complex numbers, trigonometric functions and exponents into one single formula:. The hyperbolic sine and the hyperbolic cosine. Let me try this from a different angle: Web euler’s formula, polar representation 1.
Web euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: The simple derivation uses euler's formula. Web sine and cosine are written as sums of complex exponentials. Web in complex analysis, the hyperbolic functions arise when applying the ordinary sine and cosine functions to an imaginary angle. Web euler's formula can be used to prove the addition formula for both sines and cosines as well as the double angle formula (for the addition formula, consider $\mathrm{e^{ix}}$. Web sine and cosine emerge from vector sum of three spinning numbers in euler’s formula, the green spinning number is. This formula is the most important tool in ac analysis. It is why electrical engineers need to. The number a + ib is represented by the. Web euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines.
Euler's Formula
Web sine and cosine emerge from vector sum of three spinning numbers in euler’s formula, the green spinning number is. Web euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. This formula is the most important tool in ac analysis. That is, it defines a complex number that is one unit away. Suppose we have a.
Relationship between sine, cosine and exponential function
Web sine and cosine are written as sums of complex exponentials. It is why electrical engineers need to. The complex plane complex numbers are represented geometrically by points in the plane: E i x = cos x + i sin x. Web euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines.
Direction Cosine Matrix Euler Integration Failure YouTube
Web finally, there is a nice formula discovered by leonhard euler in the 1700s that allows us to relate complex numbers, trigonometric functions and exponents into one single formula:. It is why electrical engineers need to. Web answer (1 of 9): Web euler's formula relates sine and cosine to the exponential function: Let me try this from a different angle:
Half Angles from Euler's Formula
Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒. Web sine and cosine emerge from vector sum of three spinning numbers in euler’s formula, the green spinning number.
Trigonometric Form Into A Complex Number
For example, if , then relationship to sin and cos in euler's. Web sine and cosine are written as sums of complex exponentials. Web euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. The number a + ib is represented by the. Web in complex analysis, the hyperbolic functions arise when applying the ordinary sine and.
Solved 5. Euler's equations are defined as sin (x) cos(x) e"
Web euler's formula relates sine and cosine to the exponential function: Using these formulas, we can. The hyperbolic sine and the hyperbolic cosine. Web answer (1 of 9): Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 −.
Euler's Equation
{\displaystyle e^{ix}=\cos x+i\sin x.} this formula is commonly considered for real values. The complex plane complex numbers are represented geometrically by points in the plane: Web sine and cosine are written as sums of complex exponentials. Web sine and cosine emerge from vector sum of three spinning numbers in euler’s formula, the green spinning number is. Web euler’s (pronounced ‘oilers’).
Deriving the famous Euler’s formula through Taylor Series Muthukrishnan
It is why electrical engineers need to. Web euler's formula can be used to prove the addition formula for both sines and cosines as well as the double angle formula (for the addition formula, consider $\mathrm{e^{ix}}$. Web finally, there is a nice formula discovered by leonhard euler in the 1700s that allows us to relate complex numbers, trigonometric functions and.
FileEuler's formula.svg New World Encyclopedia
The hyperbolic sine and the hyperbolic cosine. Using these formulas, we can. Web answer (1 of 9): The identities are useful in simplifying equations. Web euler's formula can be used to prove the addition formula for both sines and cosines as well as the double angle formula (for the addition formula, consider $\mathrm{e^{ix}}$.
Euler's cosine wave YouTube
Web euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. It turns messy trig identities into tidy rules for. Web in complex analysis, the hyperbolic functions arise when applying the ordinary sine and cosine functions to an imaginary angle. Web sine and cosine emerge from vector sum of three spinning numbers in euler’s formula, the green.
Web Euler’s (Pronounced ‘Oilers’) Formula Connects Complex Exponentials, Polar Coordinates, And Sines And Cosines.
Web euler's formula relates sine and cosine to the exponential function: Web answer (1 of 9): Web finally, there is a nice formula discovered by leonhard euler in the 1700s that allows us to relate complex numbers, trigonometric functions and exponents into one single formula:. The complex plane complex numbers are represented geometrically by points in the plane:
Using These Formulas, We Can.
Suppose we have a function ∠\theta=\cos\theta+i\sin\theta; Web sine and cosine are written as sums of complex exponentials. The identities are useful in simplifying equations. E i x = cos x + i sin x.
The Simple Derivation Uses Euler's Formula.
That is, it defines a complex number that is one unit away. Web sine and cosine emerge from vector sum of three spinning numbers in euler’s formula, the green spinning number is. Web euler's formula for product of cosines asked 7 years, 7 months ago modified 1 year, 10 months ago viewed 2k times 4 according to squaring the circle by ernest. The hyperbolic sine and the hyperbolic cosine.
Web Euler's Formula Relates The Complex Exponential To The Cosine And Sine Functions.
Web euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: Web euler's formula can be used to prove the addition formula for both sines and cosines as well as the double angle formula (for the addition formula, consider $\mathrm{e^{ix}}$. For example, if , then relationship to sin and cos in euler's. Let me try this from a different angle: