How To Draw The Orthocenter Of A Triangle
How To Draw The Orthocenter Of A Triangle - To draw the perpendicular or the altitude, use vertex c as the center and radius equal to the side bc. The orthocenter of a triangle is the intersection of the triangle's three altitudes. For academic help and enrichment. Use this information to help you in your geometry class! Isosceles triangle, given base and altitude. Where the triangle’s three altitudes intersect. After that, we draw the perpendicular from the opposite vertex to the line. Scroll down the page for more examples and solutions on the orthocenters of triangles. Web the orthocenter of a triangle is the point of intersection of any two of three altitudes of a triangle (the third altitude must intersect at the same spot). Proof of the pythagorean theorem.
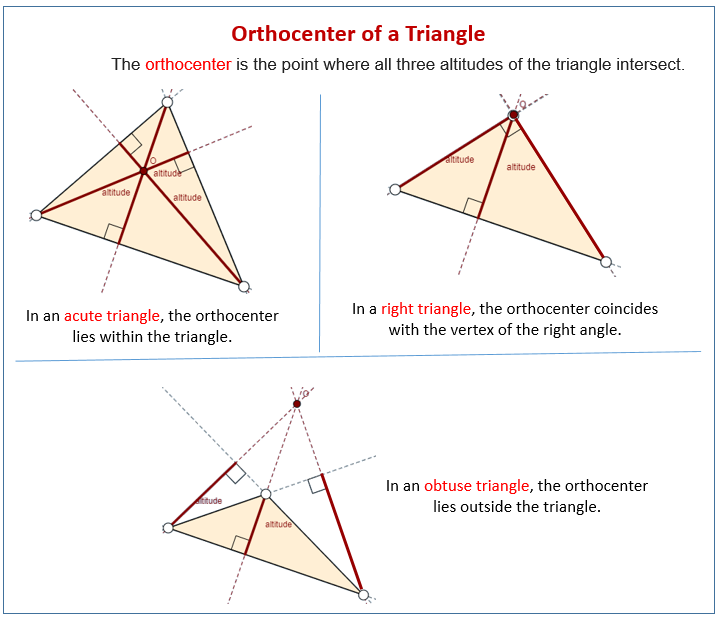
Improve your math knowledge with free questions in construct the orthocenter of a triangle and thousands of other math skills. Where all three lines intersect is the orthocenter: For an acute angle triangle, the orthocenter lies inside the triangle. See constructing the the orthocenter of a triangle. In other, the three altitudes all must intersect at a single point , and. Web the orthocenter of a triangle is the point where the altitudes of the triangle intersect. The orthocenter is typically represented by the letter h h. Proof of the pythagorean theorem. Find the slope of one side of the triangle, e.g., ab. Using this to show that the altitudes of a triangle are concurrent (at the orthocenter).
105k views 6 years ago geometry constructions. Orthocenter of a triangle is the point of intersection of all the perpendiculars to the sides of the triangle drawn from each vertex. An altitude is a line segment drawn from a vertex of the triangle p. In other, the three altitudes all must intersect at a single point , and. Web how to construct the orthocenter of a triangle with compass and straightedge or ruler. Draw a line segment (called the altitude) at right angles to a side that goes to the opposite corner. Proof of the pythagorean theorem. Isosceles triangle, given base and side. You can find where two altitudes of a triangle intersect using these four steps: An altitude is a line which passes through a vertex of the triangle and is perpendicular to the opposite side.
Orthocenter of a Triangle (examples, solutions, videos, worksheets
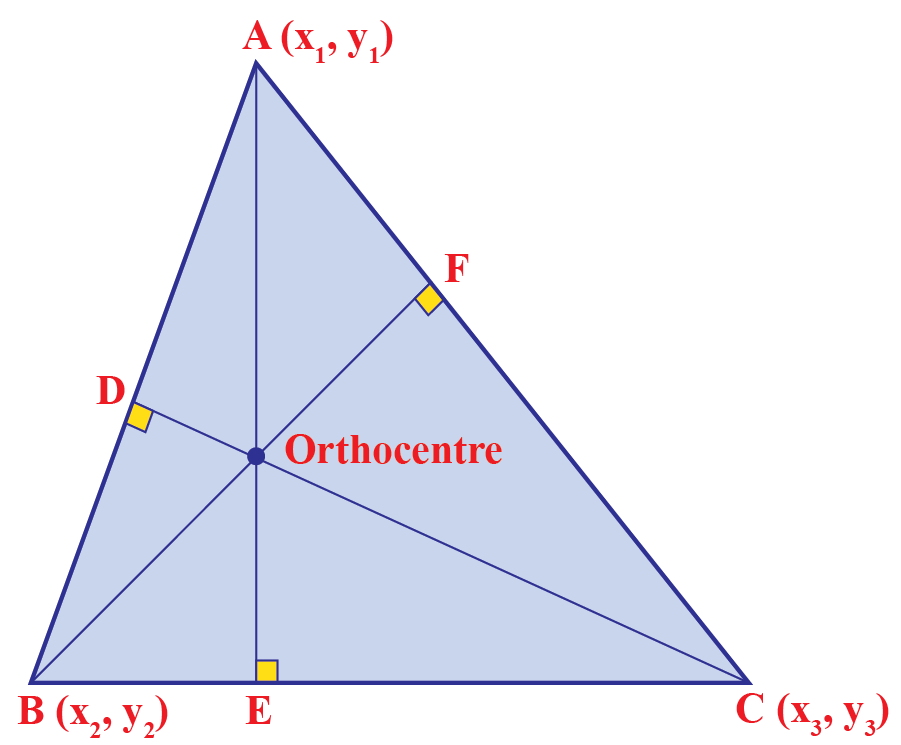
The point of intersection of the altitudes h is the orthocenter of the given triangle abc. To start, let's assume that the triangle abc has the vertex coordinates a = (x₁, y₁), b = (x₂, y₂), and c = (x₃, y₃). Isosceles triangle, given base and altitude. The following diagrams show the orthocenters of different triangles: Construct altitudes from any.
Orthocenter Definition, Properties and Examples Cuemath
Triangle altitudes are concurrent (orthocenter) google classroom. Isosceles triangle, given base and side. Find the perpendicular from any two vertices to the opposite sides. This video shows how to construct the orthocenter of a triangle by constructing altitudes of. Construct altitudes from any two vertices (a and c) to their opposite sides (bc and ab respectively).
Orthocenter Definition, Properties and Examples Cuemath
Draw arcs on the opposite sides ab and ac. Then the orthocenter is also outside the triangle. Construct altitudes from any two vertices (a and c) to their opposite sides (bc and ab respectively). Find the perpendicular from any two vertices to the opposite sides. Proof of the pythagorean theorem.
Orthocenter Definition, Properties and Examples Cuemath
Where the triangle’s three altitudes intersect. In other, the three altitudes all must intersect at a single point , and. Proof of the pythagorean theorem. Improve your math knowledge with free questions in construct the orthocenter of a triangle and thousands of other math skills. Construct an altitude from a vertex of the triangle to the opposite side, or the.
How to draw Orthocenter of a Triangle YouTube
105k views 6 years ago geometry constructions. All the perpendiculars drawn from these vertices intersect at the orthocenter. Then the orthocenter is also outside the triangle. See constructing the the orthocenter of a triangle. For academic help and enrichment.
How to Draw Altitudes of a Triangle & Orthocenter YouTube
Note that sometimes the edges of the triangle have to be extended outside the triangle to draw the altitudes. In other, the three altitudes all must intersect at a single point , and. This is because the orthocenter is the intersection of the altitudes, which are also the medians and the angle bisectors in an equilateral triangle. It has several.
Orthocenter of a triangleDefinitionFormula DewWool
Then the orthocenter is also outside the triangle. To draw the perpendicular or the altitude, use vertex c as the center and radius equal to the side bc. Web the orthocenter is one of the triangle's points of concurrency formed by the intersection of the triangle 's 3 altitudes. Web learn how to use a compass and a straightedge to.
Orthocenter of a triangleDefinitionFormula DewWool
Web the orthocenter of a triangle is the point of intersection of any two of three altitudes of a triangle (the third altitude must intersect at the same spot). Using this to show that the altitudes of a triangle are concurrent (at the orthocenter). The point of intersection of the altitudes h is the orthocenter of the given triangle abc..
Orthocenter Of A Right Triangle
Web the orthocenter of a triangle is the point where the altitudes of the triangle intersect. Find the slope of one side of the triangle, e.g., ab. It doesn't matter which vertex you start with! Web learn how to use a compass and a straightedge to construct the orthocenter of a triangle! Find the perpendicular from any two vertices to.
Orthocenter Definition, Properties and Examples Cuemath
Web the orthocenter of a triangle is the point where the altitudes of the triangle intersect. The orthocenter is the point where all three altitudes of the triangle intersect. Web the orthocenter is one of the triangle's points of concurrency formed by the intersection of the triangle 's 3 altitudes. These three altitudes are always concurrent. You can find where.
Find The Perpendicular From Any Two Vertices To The Opposite Sides.
The construction starts by extending the chosen side of the triangle in both directions. Web the orthocenter of a triangle is the point of intersection of any two of three altitudes of a triangle (the third altitude must intersect at the same spot). The orthocenter is the point where all three altitudes of the triangle intersect. Examples, solutions, videos, worksheets, games, and activities to help geometry students learn how to construct the orthocenter of a triangle.
You Can Find Where Two Altitudes Of A Triangle Intersect Using These Four Steps:
Web learn how to use a compass and a straightedge to construct the orthocenter of a triangle! Improve your math knowledge with free questions in construct the centroid or orthocenter of a triangle and thousands of other math skills. For academic help and enrichment. Draw a line segment (called the altitude) at right angles to a side that goes to the opposite corner.
Find The Slope Of One Side Of The Triangle, E.g., Ab.
Triangle altitudes are concurrent (orthocenter) google classroom. Using this to show that the altitudes of a triangle are concurrent (at the orthocenter). Then the orthocenter is also outside the triangle. It doesn't matter which vertex you start with!
Construct An Altitude From A Vertex Of The Triangle To The Opposite Side, Or The Line Containing The Opposite Side.
Isosceles triangle, given base and altitude. Web to construct the orthocenter for a triangle geometrically, we have to do the following: The orthocenter is typically represented by the letter h h. Web it is possible to construct the orthocenter of a triangle using a compass and straightedge.