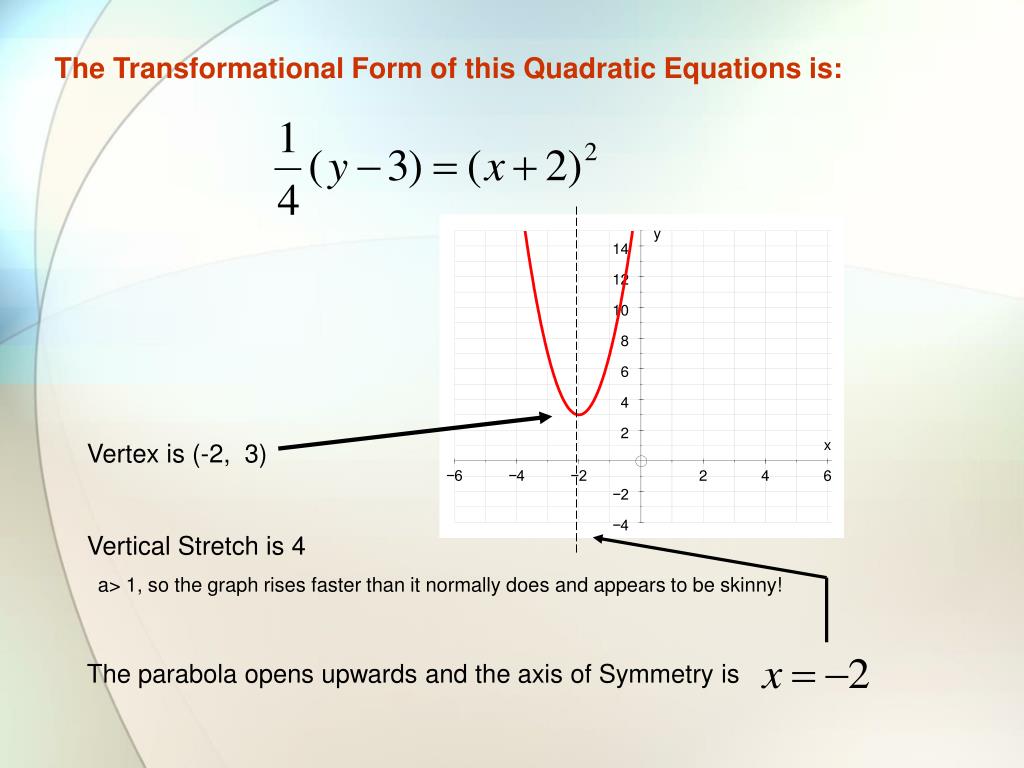
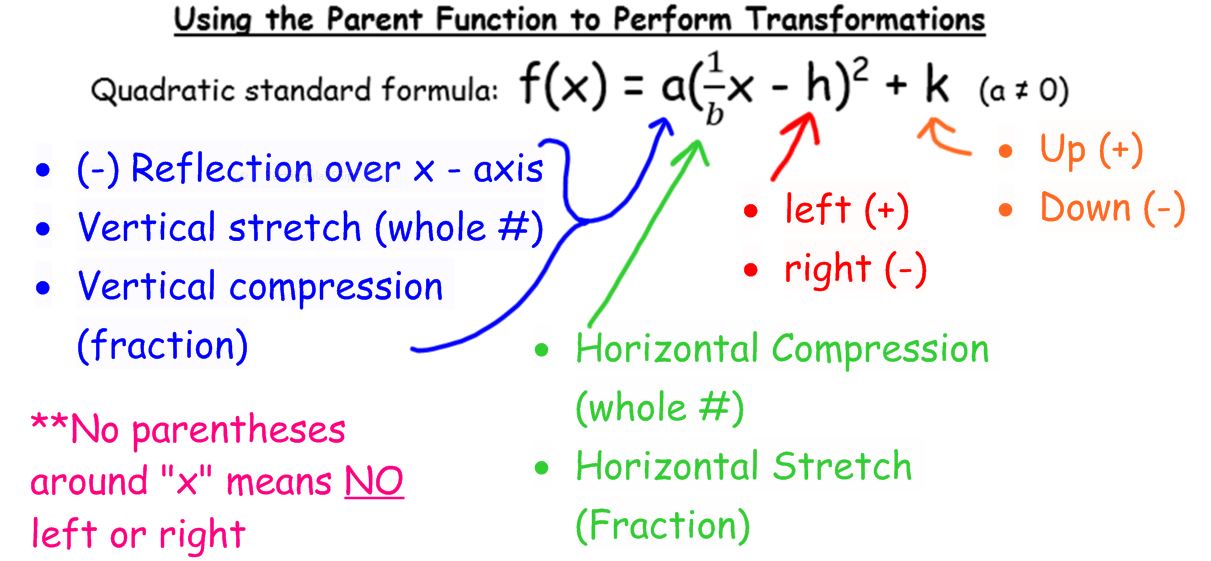
Transformational Form Of A Parabola
Transformational Form Of A Parabola - Web (map the point \((x,y)\) to the point \((\dfrac{1}{3}x, \dfrac{1}{3}y)\).) thus, the parabola \(y=3x^2\) is similar to the basic parabola. Given a quadratic equation in the vertex form i.e. Web the transformation can be a vertical/horizontal shift, a stretch/compression or a refection. Use the information provided to write the transformational form equation of each parabola. Web this problem has been solved! Y = a ( x − h) 2 + k (h,k) is the vertex as you can see in the picture below if a is positive then the parabola opens upwards like a regular u. We will call this our reference parabola, or, to generalize, our reference function. Use the information provided for write which transformational form equation of each parabola. Web sal discusses how we can shift and scale the graph of a parabola to obtain any other parabola, and how this affects the equation of the parabola. Web transformations of the parallel translations.
Use the information provided for write which transformational form equation of each parabola. Web transformations of parabolas by kassie smith first, we will graph the parabola given. Web sal discusses how we can shift and scale the graph of a parabola to obtain any other parabola, and how this affects the equation of the parabola. The (x + 3)2 portion results in the graph being shifted 3 units to the left, while the −6 results in the graph being shifted six units down. The equation of tangent to parabola y 2 = 4ax at (x 1, y 1) is yy 1 = 2a(x+x 1). The equation of the tangent to the parabola y 2 = 4ax at (at 2, 2at) is ty = x + at 2. We will talk about our transforms relative to this reference parabola. Web (map the point \((x,y)\) to the point \((\dfrac{1}{3}x, \dfrac{1}{3}y)\).) thus, the parabola \(y=3x^2\) is similar to the basic parabola. Web the vertex form of a parabola's equation is generally expressed as: First, if the reader has graphing calculator, he can click on the curve and drag the marker along the curve to find the vertex.
Web sal discusses how we can shift and scale the graph of a parabola to obtain any other parabola, and how this affects the equation of the parabola. For example, we could add 6 to our equation and get the following: The equation of tangent to parabola y 2 = 4ax at (x 1, y 1) is yy 1 = 2a(x+x 1). Web transformations of the parallel translations. If a is negative, then the graph opens downwards like an upside down u. Thus the vertex is located at \((0,b)\). The graph of y = x2 looks like this: Web the parabola is the locus of points in that plane that are equidistant from the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane parallel to another plane that is tangential to the conical surface. There are several transformations we can perform on this parabola:
PPT 5.3 Transformations of Parabolas PowerPoint Presentation, free
We can translate an parabola plumb to produce a new parabola that are resemble to the essentials paravell. Therefore the vertex is located at \((0,b)\). If a is negative, then the graph opens downwards like an upside down u. For example, we could add 6 to our equation and get the following: The equation of tangent to parabola y 2.
Standard/General Form to Transformational Form of a Quadratic YouTube
Use the information provided to write the transformational form equation of each parabola. Web (map the point \((x,y)\) to the point \((\dfrac{1}{3}x, \dfrac{1}{3}y)\).) thus, the parabola \(y=3x^2\) is similar to the basic parabola. Web these shifts and transformations (or translations) can move the parabola or change how it looks: There are several transformations we can perform on this parabola: Web.
[Solved] write the transformational form of the parabola with a focus
Web sal discusses how we can shift and scale the graph of a parabola to obtain any other parabola, and how this affects the equation of the parabola. Web this problem has been solved! If variables x and y change the role obtained is the parabola whose axis of symmetry is y. The latter encompasses the former and allows us.
Write Equation of Parabola with Horizontal Transformation YouTube
Web the transformation can be a vertical/horizontal shift, a stretch/compression or a refection. Web to preserve the shape and direction of our parabola, the transformation we seek is to shift the graph up a distance strictly greater than 41/8. The equation of tangent to parabola y 2 = 4ax at (x 1, y 1) is yy 1 = 2a(x+x 1)..
PPT Graphing Quadratic Functions using Transformational Form
The point of contact of the tangent is (x 1, y 1). Web transformations of the parabola translate. Web this problem has been solved! The equation of the tangent to the parabola y 2 = 4ax at (at 2, 2at) is ty = x + at 2. Web sal discusses how we can shift and scale the graph of a.
PPT 5.3 Transformations of Parabolas PowerPoint Presentation, free
Web the transformation can be a vertical/horizontal shift, a stretch/compression or a refection. Use the information provided to write the transformational form equation of each parabola. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane parallel to another plane that is tangential to the conical surface..
Algebra Chapter 8 Parabola Transformations YouTube
The graph of y = x2 looks like this: ∙ reflection, is obtained multiplying the function by − 1 obtaining y = − x 2. If variables x and y change the role obtained is the parabola whose axis of symmetry is y. Web we can see more clearly here by one, or both, of the following means: Completing the.
Lesson 2.1 Using Transformations to Graph Quadratic Functions Mrs. Hahn
Use the information provided for write which transformational form equation of each parabola. If a is negative, then the graph opens downwards like an upside down u. We can translate an parabola plumb to produce a new parabola that are resemble to the essentials paravell. The (x + 3)2 portion results in the graph being shifted 3 units to the.
Algebra Parabola Transformations of Quadratics y = x2 Graphs MatchUp 1
Thus the vertex is located at \((0,b)\). Therefore the vertex is located at \((0,b)\). Use the information provided for write which transformational form equation of each parabola. If variables x and y change the role obtained is the parabola whose axis of symmetry is y. Web these shifts and transformations (or translations) can move the parabola or change how it.
7.3 Parabola Transformations YouTube
Web the vertex form of a parabola's equation is generally expressed as: There are several transformations we can perform on this parabola: Y = a ( x − h) 2 + k (h,k) is the vertex as you can see in the picture below if a is positive then the parabola opens upwards like a regular u. (4, 3), axis.
We Will Talk About Our Transforms Relative To This Reference Parabola.
We will call this our reference parabola, or, to generalize, our reference function. 3 units left, 6 units down explanation: Web these shifts and transformations (or translations) can move the parabola or change how it looks: You'll get a detailed solution from a subject matter expert that helps you learn core concepts.
We Can Translate An Parabola Plumb To Produce A New Parabola That Are Resemble To The Essentials Paravell.
Web transformations of parabolas by kassie smith first, we will graph the parabola given. Web the parabola is the locus of points in that plane that are equidistant from the directrix and the focus. Web (map the point \((x,y)\) to the point \((\dfrac{1}{3}x, \dfrac{1}{3}y)\).) thus, the parabola \(y=3x^2\) is similar to the basic parabola. ∙ reflection, is obtained multiplying the function by − 1 obtaining y = − x 2.
Use The Information Provided To Write The Transformational Form Equation Of Each Parabola.
Web transformations of the parallel translations. We may translate the parabola verticals go produce an new parabola that is similar to the basic parabola. Web sal discusses how we can shift and scale the graph of a parabola to obtain any other parabola, and how this affects the equation of the parabola. Web we can see more clearly here by one, or both, of the following means:
Another Description Of A Parabola Is As A Conic Section, Created From The Intersection Of A Right Circular Conical Surface And A Plane Parallel To Another Plane That Is Tangential To The Conical Surface.
Web transformations of the parabola translate. (4, 3), axis of symmetry: The latter encompasses the former and allows us to see the transformations that yielded this graph. The point of contact of the tangent is (x 1, y 1).