Write The Equation Of The Sphere In Standard Form

Write The Equation Of The Sphere In Standard Form - X2 + y2 + z2 + 8x − 6y + 2z + 17 = 0 1 = 100% considering the first statement that 33% or 0.33 is derived from dividing. (x,y,z) = (ρcosθsinϕ,ρsinθsinϕ,ρcosϕ) where ρ is the constant radius, θ ∈ [0,2π) is the longitude. 2x2 + 2y2 + 2z2 = 4x − 20z + 1 find its center and radius. Web one common form of parametric equation of a sphere is: X2 + y2 + z2 + 8x − 6y + 4z + 20 = 0. Percentage form = 33% decimal form = 0.33 conversion factor: Web write the equation of the sphere in standard form. Write the equation of the sphere in. 2 x2 + 2 y2 + 2 z2 = 8 x − 20 z + 1 find its center and radius center ( x, y, z) radius = expert answer 1st step all steps final.

Web math calculus calculus questions and answers write the equation of the sphere in standard form. Web write the equation of the sphere in standard form. Web solved write the equation of the sphere in standard form. Web the formula for the equation of a sphere. Advanced math questions and answers. X2 + y2 + z2 + 8x − 6y + 2z + 17 = 0 Web one common form of parametric equation of a sphere is: Web join subscribe 144 share save 14k views 8 years ago calculus iii exam 1 please subscribe here, thank you!!! 2x2 + 2y2 + 2z2 = 4x − 20z + 1 find its center and radius. Web math calculus calculus questions and answers write the equation of the sphere in standard form.

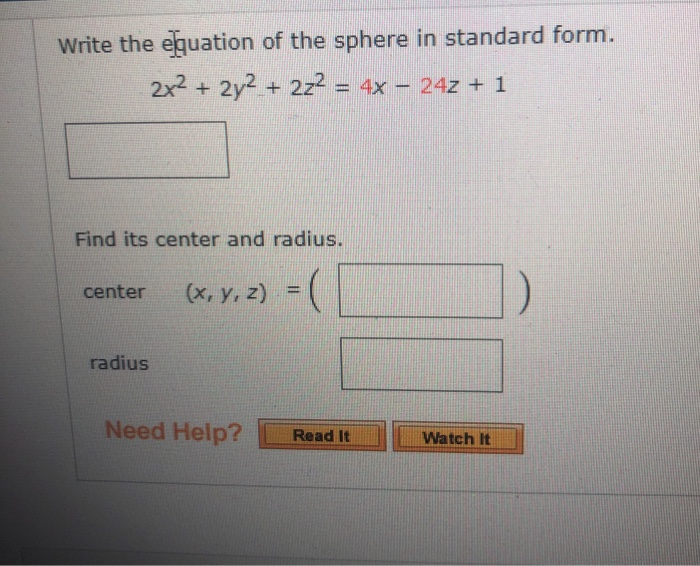
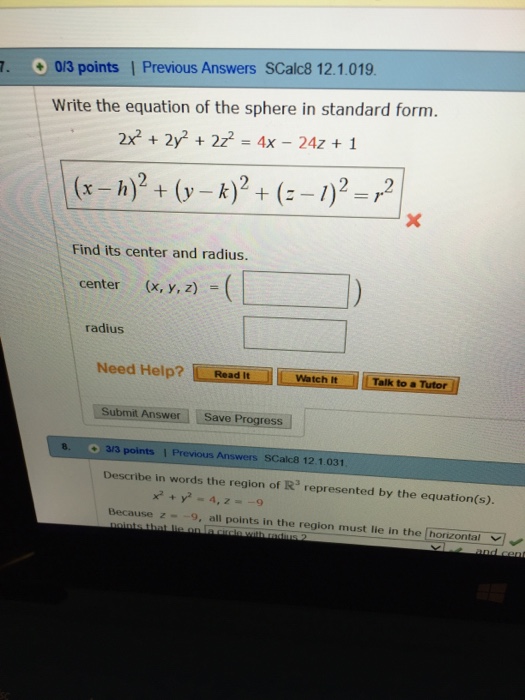
Write the equation of the sphere in. Web write the equation of the sphere in standard form. Center (x, y, z) = radius this problem has been solved! 2x2 + 2y2 + 2z2 = 4x − 24z + 1 find its center and radius. X2 + y2 + z2 + 8x − 6y + 2z + 17 = 0 Web solved write the equation of the sphere in standard form. X2 + y2 + z2 + 4x − 2y − 4z = 16 find its center and radius. Web the general equation of the sphere is x2 + y2 + z2 = r2 and in this article, we will learn about deriving the equation of a sphere along with its volume and surface. X2 + y2 + z2 + 8x − 6y + 6z + 25 = 0 find its center and radius. Web learn how to write the standard equation of a sphere given the center and radius.

How can we Write the Equation of a Sphere in Standard Form? [Solved]

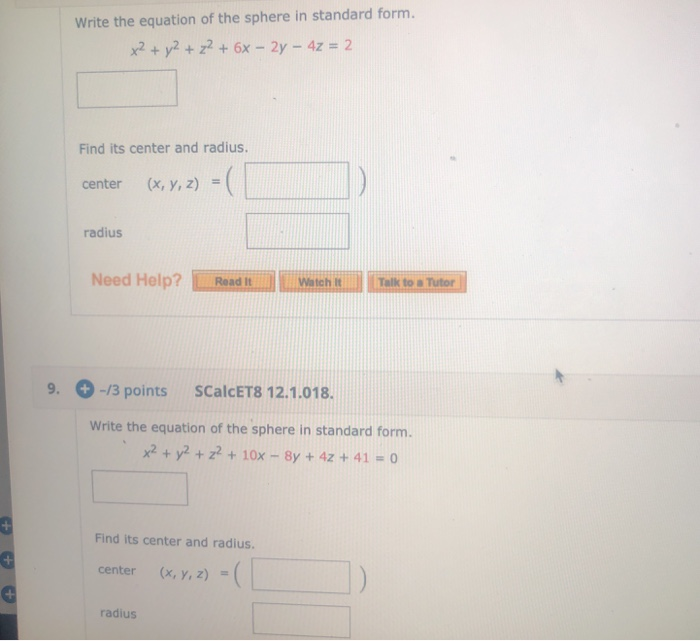
X2 + y2 + z2 + 4x − 2y − 4z = 16 find its center and radius. Also learn how to identify the center of a sphere and the radius when given. Web write the equation of the sphere in standard form. Web one common form of parametric equation of a sphere is: (x,y,z) = (ρcosθsinϕ,ρsinθsinϕ,ρcosϕ) where ρ is.

Equation of the Sphere in Standard Form, Center, and Radius YouTube

Advanced math questions and answers. Center (x, y, z) = radius this problem has been solved! Web learn how to write the standard equation of a sphere given the center and radius. Web write the equation of the sphere in standard form. 2x2 + 2y2 + 2z2 = 4x − 24z + 1 find its center and radius.

Question Video Finding the Equation of a Sphere That Passes through

(x,y,z) = (ρcosθsinϕ,ρsinθsinϕ,ρcosϕ) where ρ is the constant radius, θ ∈ [0,2π) is the longitude. 2x2 + 2y2 + 2z2 = 4x − 24z + 1 find its center and radius. Web write the equation of the sphere in standard form. X2 + y2 + z2 + 8x − 6y + 2z + 17 = 0 Web join subscribe 144.

Equation Of A Sphere ShareTechnote / Find the energy of the

Web join subscribe 144 share save 14k views 8 years ago calculus iii exam 1 please subscribe here, thank you!!! X2 + y2 + z2 + 8x − 6y + 4z + 20 = 0. Web one common form of parametric equation of a sphere is: 2 x2 + 2 y2 + 2 z2 = 8 x − 20 z.

Solved Write the equation of the sphere in standard form.

X2 + y2 + z2 + 8x − 6y + 2z + 17 = 0 Web math calculus calculus questions and answers write the equation of the sphere in standard form. (x,y,z) = (ρcosθsinϕ,ρsinθsinϕ,ρcosϕ) where ρ is the constant radius, θ ∈ [0,2π) is the longitude. 2x2 + 2y2 + 2z2 = 4x − 24z + 1 find its center.

Solved Write the equation of the sphere in standard form. x2

X2 + y2 + z2 + 8x − 6y + 2z + 17 = 0 X 2 + y 2 + z 2 + a x + b y + c z + d = 0, this is. Web join subscribe 144 share save 14k views 8 years ago calculus iii exam 1 please subscribe here, thank you!!! (x,y,z) =.

Solved Write the equation of the sphere in standard form.

X2 + y2 + z2 + 8x − 6y + 2z + 17 = 0 Write the equation of the sphere in. Web write the equation of the sphere in standard form. Web write the equation of the sphere in standard form. X 2 + y 2 + z 2 + a x + b y + c z +.

Solved Write the equation of the sphere in standard form.

X2 + y2 + z2 + 4x − 2y − 4z = 16 find its center and radius. Web write the equation of the sphere in standard form. Web write the equation of the sphere in standard form. Web write the equation of the sphere in standard form. X2 + y2 + z2 + 8x − 6y + 6z +.

Solved Write the equation of the sphere in standard form.

X2 + y2 + z2 + 8x − 6y + 6z + 25 = 0 find its center and radius. Web the general equation of the sphere is x2 + y2 + z2 = r2 and in this article, we will learn about deriving the equation of a sphere along with its volume and surface. Center (x, y, z) =.

Solved Write the equation of the sphere in standard form.

Percentage form = 33% decimal form = 0.33 conversion factor: Web write the equation of the sphere in standard form. Center (x, y, z) = radius this problem has been solved! Advanced math questions and answers. X2 + y2 + z2 + 8x − 6y + 4z + 20 = 0.

Web Math Calculus Calculus Questions And Answers Write The Equation Of The Sphere In Standard Form.

Web write the equation of the sphere in standard form. 2 x2 + 2 y2 + 2 z2 = 8 x − 20 z + 1 find its center and radius center ( x, y, z) radius = expert answer 1st step all steps final. Web math calculus calculus questions and answers write the equation of the sphere in standard form. 1 = 100% considering the first statement that 33% or 0.33 is derived from dividing.

Web Write The Equation Of The Sphere In Standard Form.

2x2 + 2y2 + 2z2 = 4x − 24z + 1 find its center and radius. X 2 + y 2 + z 2 + a x + b y + c z + d = 0, this is. Write the equation of the sphere in. Web learn how to write the standard equation of a sphere given the center and radius.

X2 + Y2 + Z2 + 12X − 8Y + 2Z + 44 = 0 Then Find Its Center And Radius This Problem Has Been Solved!

Web the formula for the equation of a sphere. Percentage form = 33% decimal form = 0.33 conversion factor: X2 + y2 + z2 + 4x − 2y − 4z = 16 find its center and radius. Web write the equation of the sphere in standard form.

X2 + Y2 + Z2 + 8X − 6Y + 4Z + 20 = 0.

Web write the equation of the sphere in standard form. Web join subscribe 144 share save 14k views 8 years ago calculus iii exam 1 please subscribe here, thank you!!! X2 + y2 + z2 + 8x − 6y + 2z + 17 = 0 Advanced math questions and answers.