Drawer Principle
Drawer Principle - Web pigeonhole principle is one of the simplest but most useful ideas in mathematics. Web important mathematical device has such an informal name, use instead the term dirichlet drawer principle. Average number of pigeons per hole = (kn+1)/n = k. Web theorem 1.6.1 (pigeonhole principle) suppose that n + 1 (or more) objects are put into n boxes. This seemingly trivial statement may be used with remarkable creativity to generate striking counting arguments, especially in olympiad settings. The solution relies on the pigeonhole. Let s s be a finite set whose cardinality is n n. This is also known as the dirichlet’s drawer principle or dirichlet’s box principle after the mathematician peter gustav dirichlet. Lastly, we should note that, with eight cards drawn, it is possible to have exactly two cards of each suit, so the minimum number is indeed 9.\ _\square 9. If (kn+1) pigeons are kept in n pigeon holes where k is a positive integer, what is the average no.
Assume a flock of 25 pigeons roosting in a collection of 24. Average number of pigeons per hole = (kn+1)/n = k. You might end up with one red, one green, and one blue. This is also known as the dirichlet’s drawer principle or dirichlet’s box principle after the mathematician peter gustav dirichlet. In 1834, johann dirichlet noted that if there are five objects in four drawers then there is a drawer with two or more objects. The solution relies on the pigeonhole. In older texts, the principle may be. For this reason it is also commonly called dirichlet's box. Then some box contains at least two objects. A ppearing as early as 1624, the pigeonhole principle also called dirichlet’s box principle, or dirichlet’s drawer principle points out.
The solution relies on the pigeonhole. Average number of pigeons per hole = (kn+1)/n = k. If (kn+1) pigeons are kept in n pigeon holes where k is a positive integer, what is the average no. Web drawer principle is an important basic theory in combinatorics.this paper introduced common forms of drawer principle,and discussed the application of this principle by means of concrete examples in algebraic problem,number theory problem and geometric problem. A ppearing as early as 1624, the pigeonhole principle also called dirichlet’s box principle, or dirichlet’s drawer principle points out. Informally it says that if n +1 or more pigeons are placed in n holes, then some hole must have at least 2 pigeons. It is a surprisingly powerful and useful device. Web 14.8 the pigeonhole principle here is an old puzzle: Web dirichlet’s principle by 1840 it was known that if s ⊂ r is a closed and bounded set and f : Web in the 1800s, german mathematician peter gustave lejeune dirichlet proposed the pigeonhole principle, also known as the dirichlet principle, which states that if there are m boxes or drawers and n > m objects, at least one of the boxes must contain multiple objects.
THE PIGEON HOLE PRINCIPLE or also known as DRAWER PRINCIPLE BY ALVIN
Assume a flock of 25 pigeons roosting in a collection of 24. Web the first formalization of the pigeonhole concept is believed to have been made by dirichlet in the 1800s as what he called schubfachprinzip or the “drawer/shelf principle.” the first appearance of the term “pigeonhole principle” was used by mathematician raphael m. Of pigeons per pigeon hole? Web.
DRAWER MAKING Woodworking, Drawers, Wood joinery
This seemingly simple fact can be used in surprising ways. Web in the 1800s, german mathematician peter gustave lejeune dirichlet proposed the pigeonhole principle, also known as the dirichlet principle, which states that if there are m boxes or drawers and n > m objects, at least one of the boxes must contain multiple objects. The pigeonhole principle, also known.
Level 17 Probability Theory and Statis… Memrise
Then the total number of objects is at most 1 + 1 + ⋯ + 1 = n, a contradiction. Web although the pigeonhole principle appears as early as 1624 in a book attributed to jean leurechon, [2] it is commonly called dirichlet's box principle or dirichlet's drawer principle after an 1834 treatment of the principle by peter gustav lejeune.
Drawer Making Woodworking Masterclasses
This was first stated in 1834 by dirichlet. Web dirichlet’s principle by 1840 it was known that if s ⊂ r is a closed and bounded set and f : The schubfachprinzip, or drawer principle, got renamed as the pigeonhole principle, and became a powerful tool in mathematical proofs.in this demonstration, pigeons land in a park. Web the pigeonhole principle.
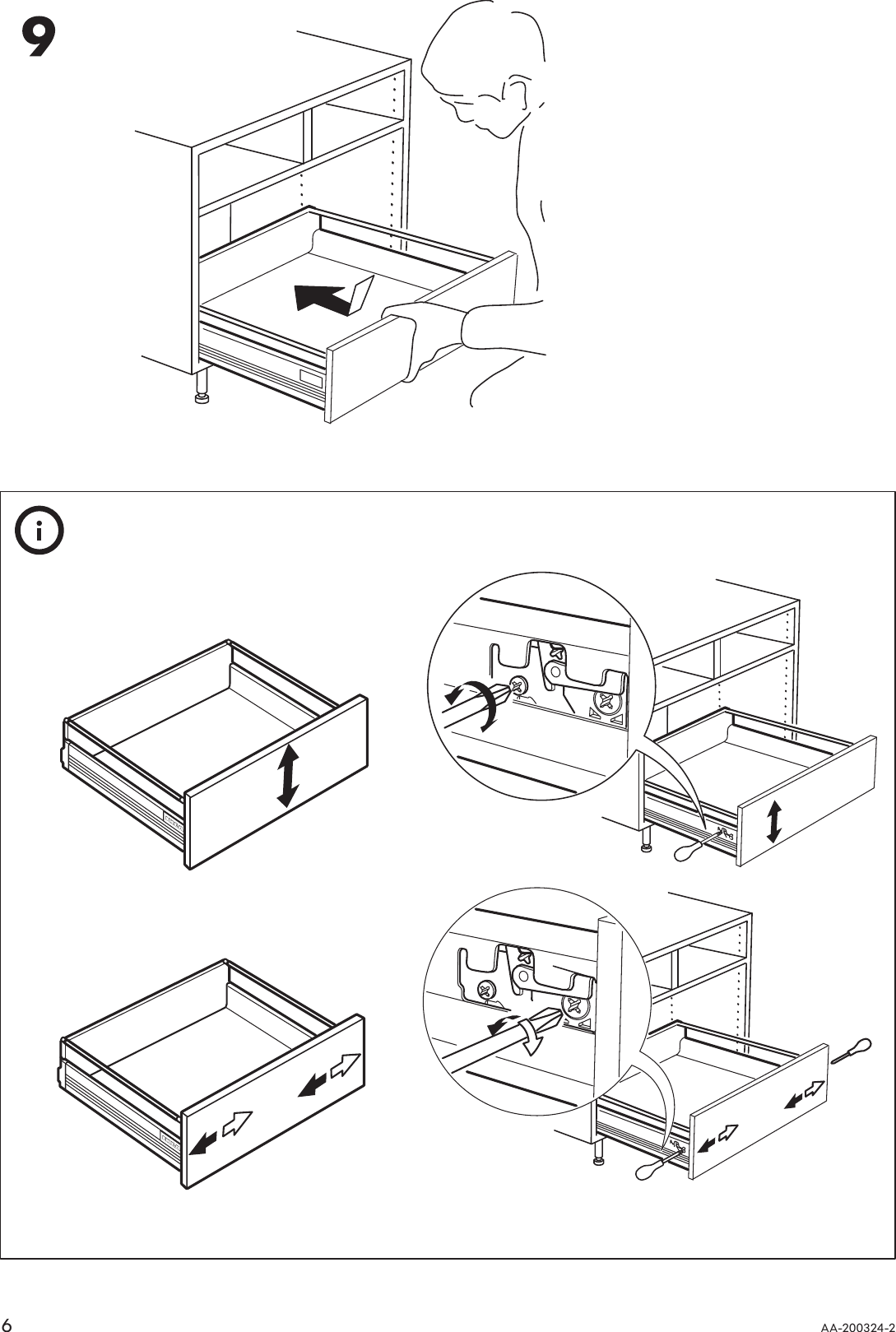
Ikea Rationell Deep Full Extending Drawer 30 Assembly Instruction
Web 14.8 the pigeonhole principle here is an old puzzle: Web theorem 1.6.1 (pigeonhole principle) suppose that n + 1 (or more) objects are put into n boxes. Label the boxes by the pairs'' (e.g., the red pair, the blue pair, the argyle pair,…). It is a surprisingly powerful and useful device. Web important mathematical device has such an informal.
8 Kitchen Renovation Essentials Wallspan Kitchens and Wardrobes
Web the first formalization of the idea is believed to have been made by peter gustav lejeune dirichlet in 1834 under the name schubfachprinzip (drawer principle or shelf principle). Assume a flock of 25 pigeons roosting in a collection of 24. In 1834, johann dirichlet noted that if there are five objects in four drawers then there is a drawer.
THE PIGEON HOLE PRINCIPLE or also known as DRAWER PRINCIPLE BY ALVIN
It is a surprisingly powerful and useful device. Of pigeons per pigeon hole? Web 14.8 the pigeonhole principle here is an old puzzle: The examples in this paper are meant to convince you of this. Picking 6 socks guarantees that at least one pair is chosen.
Kitchen Design Principles Home Design Tutorials
How many socks must you withdraw to be sure that you have a matching pair? A ppearing as early as 1624, the pigeonhole principle also called dirichlet’s box principle, or dirichlet’s drawer principle points out. For this reason it is also commonly called dirichlet's box. Lastly, we should note that, with eight cards drawn, it is possible to have exactly.
Prove that there are three people in any of the six people who know
Informally it says that if n +1 or more pigeons are placed in n holes, then some hole must have at least 2 pigeons. It has explained everything from the amount of hair on people's heads to fundamental principles of. Given boxes and objects, at least one box must contain more than one object. If (kn+1) pigeons are kept in.
GRASS's interzum Debut Nova Pro Scala Always an Idea Different
Web dirichlet’s principle by 1840 it was known that if s ⊂ r is a closed and bounded set and f : This seemingly trivial statement may be used with remarkable creativity to generate striking counting arguments, especially in olympiad settings. The examples in this paper are meant to convince you of this. Web the first formalization of the idea.
Web Pigeonhole Principle Is One Of The Simplest But Most Useful Ideas In Mathematics.
Do not be misled by the simplicity of this principle; The examples in this paper are meant to convince you of this. Web in the 1800s, german mathematician peter gustave lejeune dirichlet proposed the pigeonhole principle, also known as the dirichlet principle, which states that if there are m boxes or drawers and n > m objects, at least one of the boxes must contain multiple objects. Let s s be a finite set whose cardinality is n n.
The Schubfachprinzip, Or Drawer Principle, Got Renamed As The Pigeonhole Principle, And Became A Powerful Tool In Mathematical Proofs.in This Demonstration, Pigeons Land In A Park.
Given n boxes and m > n objects, at least one box must contain more than one object. This is also known as the dirichlet’s drawer principle or dirichlet’s box principle after the mathematician peter gustav dirichlet. If (kn+1) pigeons are kept in n pigeon holes where k is a positive integer, what is the average no. S → r is a continuous function, then there are points p and q in s where f has its maximum and minimum value.
How Many Socks Must You Withdraw To Be Sure That You Have A Matching Pair?
It is a surprisingly powerful and useful device. It has explained everything from the amount of hair on people's heads to fundamental principles of. Web dirichlet’s principle by 1840 it was known that if s ⊂ r is a closed and bounded set and f : Picking 6 socks guarantees that at least one pair is chosen.
Lastly, We Should Note That, With Eight Cards Drawn, It Is Possible To Have Exactly Two Cards Of Each Suit, So The Minimum Number Is Indeed 9.\ _\Square 9.
Assume a flock of 25 pigeons roosting in a collection of 24. A ppearing as early as 1624, the pigeonhole principle also called dirichlet’s box principle, or dirichlet’s drawer principle points out. Of pigeons per pigeon hole? Label the boxes by the pairs'' (e.g., the red pair, the blue pair, the argyle pair,…).